Modelos de Volatilidad

Las series de tiempo financieras se caracterizan, entre otras cosas, por la agrupación de la volatilidad. Es decir, hay periodos de relativa calma que son interrumpidos por estallidos de volatilidad.

Es común que en las instituciones financieras se mida el riesgo de sus actividades mediante un valor en riesgo (VaR). Para ello, generalmente usan un nivel de confianza del 99% durante un horizonte de 10 días de negocios. 

Inicialmente vamos a analizar la serie de rendimientos semanales del USDCOP, mediante una prueba de estacionariedad y un modelo ARMA para los retornos. Luego vamos a comprobar la presencia de efectos ARCH. Finalmente vamos estimar un modelo EGARCH, haremos el gráfico de sonrisa de volatilidad, un backtesting con VaR del 99% y pronosticaremos la volatilidad para los próximos 10 días.

Para descargar los datos vamos a usar la librería "quantmod", para pruebas de raíz unitaria la librería ''urca'' y para los modelos de la familia GARCH la librería "rugarch". Si no tienes estas  librerías, puedes instalarlas con el comando

install.packages(c("quantmod",''urca'',"rugarch")) 

Para cargar los paquetes, escribe:

library(quantmod)
library(urca)
library(rugarch).

Para obtener la serie de precios durante 8 años, debemos recordar que la fuente de datos "oanda" solo permite descargas de máximo 5 años. Así que obtendremos los datos en dos partes (usd1 y usd2) y luego las juntamos en una sola variable (usd) mediante la función rbind(). La función as.xts() ayuda a convertir los datos en series de tiempo indizadas por fechas. Luego la función to.weekly() nos ayudará a convertir la serie de precios diarios a precios semanales en formato OHLC (apertura, máximo, mínimo, cierre). Por último obtenemos la serie de rendimientos logarítmicos de los precios de cierre, y eliminaremos el primer dato, ya que éste se pierde al diferenciar una vez:

getFX("USD/COP", from="2012-01-01", to="2016-06-01") 
usd1 = USDCOP[,1]
getFX("USD/COP", from="2007-12-31", to="2011-12-31")
usd2 = USDCOP[,1]
usd = as.xts(rbind(usd2,usd1))
usd.sem = to.weekly(usd)
r = diff(log(usd.sem[,4]))[-1]

Estacionariedad

Siguiendo el procedimiento descrito en Modelos lineales de series de tiempo y predicción, podemos determinar si los retornos siguen un proceso I(0). 

r.adf = ur.df(r,type="none")

summary(r.adf) 

El resultado es que se rechaza la hipótesis nula de existencia de una raiz unitaria a un nivel de significancia del 5%. Por lo tanto es un proceso estacionario. (Después de realizar type=''trend'', y type=''drift'', y verificando que no son significativos los coeficientes para la tendencia y la constante)

Dependencia lineal de los retornos

Siguiendo el procedimiento descrito en Modelos lineales de series de tiempo y predicción, podemos encontrar un modelo ARMA para la serie de retornos. 

especificaciones = arfimaspec(
  mean.model = list(armaOrder = c(12,0), include.mean = TRUE),
  distribution.model = "norm",
  fixed.pars = list(mu=0,ar1=0,ar2=0,ar3=0,ar6=0,ar7=0,ar8=0,
     ar9=0,ar10=0,ar11=0))
mod = arfimafit(especificaciones, r)
mod

La salida de este modelo nos muestra que los parámetros son significativos (para un 5% de significancia). Resolviendo por máxima verosimilitud, los parámetros óptimos son: (omitiendo los demás resultados)

Optimal Parameters
---------------------------------------------------------------------------
        Estimate  Std.   Error         t value        Pr(>|t|)
ar4       0.124787    0.047153   2.6464     0.008134
ar5       0.097820    0.047285   2.0687     0.038570
ar12     0.113640    0.047726   2.3811     0.017262

Veamos si los residuales del modelo son ruido blanco:

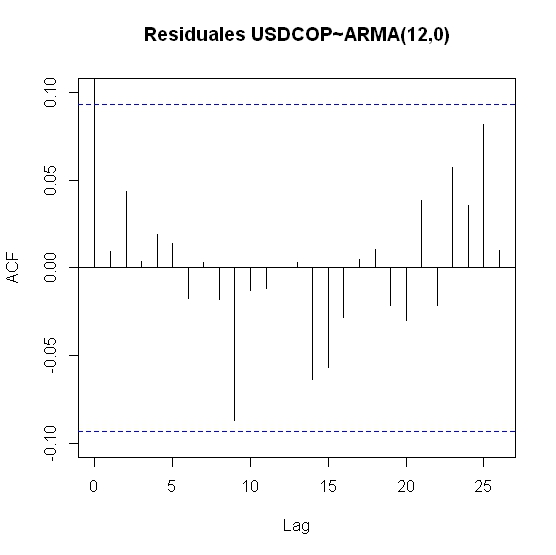
acf(residuals(mod),ylim=c(-0.1,0.1),main="Residuales USDCOP~ARMA(12,0)")

Los coeficientes de autocorrelación de los residuales del modelo se encuentran dentro de las bandas de aceptación. Por lo que los errores distribuyen ruido blanco.

Comprobación de efectos ARCH

Correlograma de los retornos al cuadrado

Podemos obtener una aproximación de la volatilidad por medio del cuadrado de los retornos, y observar si hay autocorrelaciones significativas:

acf(residuals(mod)^2,main="Residuales^2")

Encontramos que el modelo ARMA(12,0) no captura la dinámica de la volatilidad, ya que existe coeficientes de autocorrelación significativos entre los errores al cuadrado. Ésto nos indica la presencia de efectos ARCH.

Estadístico de prueba

Podemos realizar la prueba Ljung-Box (Prueba conjunta) para determinar si el cuadrado de los retornos distribuye ruido blanco:

Box.test(residuals(mod)^2,type="Ljung-Box")

        Box-Ljung test

data:  residuals(mod)^2
X-squared = 18.355, df = 1, p-value = 1.834e-05

Dado un valor-p inferior al 5% de significancia, podemos rechazar la hipótesis nula de no autocorrelación en el cuadrado de los retornos. Esto nos indica presencia de efectos ARCH, y por tanto, un modelo de la familia GARCH debe ser estimado.

Modelo de la familia GARCH

Especificación del modelo

Debemos especificar el modelo mediante la función ugarchspec().  Vamos a especificar un modelo EGARCH y luego se explicará cada argumento usado.

spec1 = ugarchspec(
  distribution.model = "ged",
  variance.model = list(model="eGARCH", garchOrder = c(1,1)),
  mean.model = list(armaOrder = c(0,0),  include.mean = TRUE) )

• distribution.model es una cadena que permite indicar la densidad condicional para las innovaciones (se puede elegir entre norm, std, ged, snorm, sstd, sged, nig, ghyp, jsu). 
• mean.model debe ser una lista que contenga las especificaciones del modelo para la media. Dentro de esta lista, hay dos argumentos importantes que deben ser tenidos en cuenta: 
• armaOrder debe ser un vector de dos dimensiones. El primer elemento es el máximo orden de la parte AR y el segundo elemento es el máximo orden de la parte MA. 
• include.mean  es un booleano que indica si se debe incluir la media.
• variance.model debe ser una lista que contenga las especificaciones del modelo para la volatilidad. Dentro de esta lista, hay varios argumentos importantes que pueden ser modificados:
• model es una cadena que indica el tipo de modelo. Puede ser “sGARCH”, “fGARCH”, “eGARCH”,“gjrGARCH”, “apARCH”, “iGARCH” y “csGARCH”.
• garchOrder es un vector de dos dimensiones. El primer elemento es el máximo orden (p) de la parte GARCH y el segundo elemento es el máximo orden (q) de la parte ARCH.
• submodel solo en caso de que el argumento model sea fGARCH, se acepta “GARCH”, “TGARCH”,“AVGARCH”, “NGARCH”, “NAGARCH”, “APARCH”,“GJRGARCH” y “ALLGARCH”.
• fixed.pars debe ser una lista que contenga los parámetros que permanecerán fijos durante la optimización.

Podemos observar que la media del modelo es un ARMA(0,0) debido a que bajo el modelo EGARCH, los parámetros del modelo ARMA(12,0) no eran significativos en la estimación. Cada uno se fue eliminando de acuerdo al que presentara mayor valor-p.

Estimación del modelo

Para estimar algún modelo de la familia GARCH mediante el método de máxima verosimilitud, se usa la función ugarchfit(). El argumento data indica el vector de la serie de tiempo a analizar. El argumento spec recibe la especificación del modelo.

mod1 = ugarchfit(data=r, spec = spec1)

si queremos ver la salida escribimos mod1. Podemos encontrar que los parámetros son significativos a un nivel del 5%. Encontraremos muchos otros datos importantes como el valor de la función de probabilidad logarítmica y los criterios de información.

Optimal Parameters

---------------------------------------------------------------

             Estimate  Std.        Error            t value          Pr(>|t|)

mu            0.000742         0.000350         2.1217     0.033862

omega     -0.085386         0.022163       -3.8527     0.000117

alpha1      0.051751         0.024289         2.1306     0.033119

beta1        0.989620         0.002723    363.4813     0.000000

gamma1    0.128675         0.045317        2.8395     0.004519

shape        1.266618         0.113018      11.2072     0.000000

Comprobación del modelo

Podemos trazar un correlograma de los errores estandarizados mediante la función plot(), la cual nos muestra 12 opciones para escoger de forma interactiva. O mediante el argumento which podemos indicar cual de esas 12 opciones queremos ver. Por ejemplo la opción 10 nos muestra la ACF de los errores estandarizados, la opción 11 nos muestra la ACF del cuadrado de los errores estandarizados.

plot(mod1,which=10)

Vemos que los coeficientes de autocorrelación se encuentran dentro de las bandas de aceptación para un nivel de significancia del 5%. 

plot(mod1,which=11)

Sonrisa de Volatilidad

Es posible realizar la curva de impactos mediante el comando plot() y escogiendo la opción 12.

plot(mod1,which=12)

De acuerdo a este gráfico, las noticias positivas (que afectan al usdcop en sentido alcista, como por ejemplo una caída del petróleo) generan un efecto mayor en la volatilidad que las noticias negativas de igual magnitud

Backtesting del Modelo de Riesgo

La función ugarchroll() realiza un backtest histórico (pronóstico dentro de la muestra) sobre el modelo GARCH especificado:

test = ugarchroll(spec1, r, n.start=200,refit.every=1,refit.window="moving",

solver="hybrid",calculate.VaR = TRUE, VaR.alpha=0.01,keep.coef=TRUE)

Esta operación es costosa computacionalmente. En un procesador intel Celeron D se tardó al rededor de 20 minutos. el argumento n.start indica que comenzará el backtest desde el periodo 200. El argumento refit.every indica que se recalculará la estimación cada semana (un periodo a la vez). refit.window indica una ventana móvil que utiliza todos los datos anteriores para la primera estimación y luego se traslada en una longitud igual a refit.every (a menos que se use window.size en su lugar). solver indica el tipo de algoritmo a usar para resolver el problema.  calculate.VaR indica si se debe estimar el valor en riesgo (VaR) durante la estimación. VaR.alpha indica el nivel de significancia para estimar el VaR. keep.coef indica si se quiere mantener  los coeficientes estimados.

Si queremos ver el resultado de la predicción del VaR usamos la función plot()

plot(test,which=4)

Para ver la volatilidad pronosticada en el backtest y la volatilidad real (en valor absoluto), usamos la opción 2:

plot(test,which=2)

Predicción del modelo de Volatilidad

Una vez que el backtest muestra que el modelo de riesgo funciona correctamente, podemos realizar predicciones del VaR. La función ugarchforecast() toma como argumentos el modelo especificado y el número de periodos a pronosticar fuera de la muestra. 

pron =  ugarchforecast(mod1, n.ahead=10)

pron

        Series        Sigma

T+1  0.0007418    0.02322

T+2  0.0007418    0.02314

T+3  0.0007418    0.02306

T+4  0.0007418    0.02298

T+5  0.0007418    0.02289

T+6  0.0007418    0.02281

T+7  0.0007418    0.02274

T+8  0.0007418    0.02266

T+9  0.0007418    0.02258

T+10 0.0007418    0.02251

Si queremos encontrar el VaR del 99% estimado para el periodo T+1, asumiendo una distribución normal, calculamos el cuantil 99 de la distribución normal estándar  y lo multiplicamos por la volatilidad, esto es:

qnorm(0.99)*0.02322

0.0540178

Podemos realizar un gráfico del pronóstico de los retornos y del pronóstico de la volatilidad:

plot(pron,which=1)

plot(pron,which=3)

Hasta aquí el recorrido por los modelos de series de tiempo. Espero sea de utilidad y cualquier comentario es bienvenido.