Análisis de Series de Tiempo

El análisis de series de tiempo se refiere a los datos obtenidos en función del tiempo. Las observaciones contiguas son típicamente dependientes. El análisis de series de tiempo se ocupa de crear técnicas para capturar estas dependencias.

El objetivo de esta publicación es introducir algunas técnicas de modelado comunes. Vamos a  ver como usar R para resolver ejemplos del mundo real. Comenzaremos con algunas estrategias para procesar series de tiempo en R, luego en otras publicaciones posteriores nos ocuparemos de los modelos lineales de series de tiempo y la forma en la que pueden ser usados para pronosticar, algunas nociones de cointegración y finalmente algunos modelos de volatilidad para gestión de riesgos.

Manejando series temporales con R

Para comenzar, descargaremos los datos de Facebook con ayuda de la librería quantmod y obtenemos una primera impresión de los datos con un gráfico de velas:

library(quantmod)
getSymbols("FB")
chartSeries(FB)

Cuando se trata de series de tiempo, es más interesante ver los retornos que los precios. Ésto es porque los retornos son generalmente estacionarios. Así que vamos a calcular los retornos de los precios de cierre, y para ello contamos con varias opciones. Una forma es calcularlo con su fórmula habitual:

$${ r }_{ t }\quad =\log { { P }_{ t } } -\quad \log { { P }_{ t-1 } } =\quad \log { \frac { { P }_{ t } }{ { P }_{ t-1 } } }$$
r = diff(log(FB[,4])) # la columna 4 es la de cierre
chartSeries(r) 

Con ésto es suficiente para el análisis. Sin embargo, la otra forma es calcularlo mediante una función que trae la librería quantmod llamada Delt().

r = Delt(FB[,4], type="log") # el tipo también puede ser "arithmetic"

Esta función, aunque arroja los mismos resultados, es útil para otras cosas más como calcular la diferencia entre dos precios distintos:

r2 = Delt(FB[,4],FB[,1], type="log") # diferencia entre el precio de cierre y el precio de apertura
head(r2)
                 Delt.0.log
2012-05-18  0.095238815
2012-05-21  0.070891354
2012-05-22  0.050631816
2012-05-23 -0.019883849
2012-05-24 -0.002424918
2012-05-25  0.030553278

O también para calcular la diferencia entre dos precios distintos y en periodos de tiempo distintos:

r2 = Delt(FB[,4],FB[,1],k=0:2, type="log")
head(r2)
                 Delt.0.log       Delt.1.log      Delt.2.log
2012-05-18  0.095238815           NA               NA
2012-05-21  0.070891354 -0.045486734          NA
2012-05-22  0.050631816 -0.042623439 -0.15900153
2012-05-23 -0.019883849  0.011864850 -0.08139041
2012-05-24 -0.002424918  0.029255388  0.06100409

Ahora veremos el resumen de los datos mediante la función summary() y si no queremos ver las fechas usamos la función coredata():

> summary(coredata(r))
              FB.Close        
 Min.      :-0.124369  
 1st Qu.  :-0.011024  
 Median  : 0.001025  
 Mean     : 0.001089  
 3rd Qu.  : 0.013185  
 Max.      : 0.259371  
 NA's      :1 

Para saber la fecha del rendimiento mínimo usamos la función which.min(r) que nos devuelve el número del elemento que contiene el valor mínimo buscado. Para saber la fecha del elemento lo buscamos con r[numeroElemento]. Combinando ambas funciones en una sola línea obtenemos lo que deseamos:

> r[which.min(r)]
                  FB.Close
2012-07-27 -0.124369

Una búsqueda rápida en internet revela que Facebook el día viernes 27 de Julio del 2012 se desplomó a su nivel más bajo. Justo un día después de que reveló sus estados financieros por primera vez.

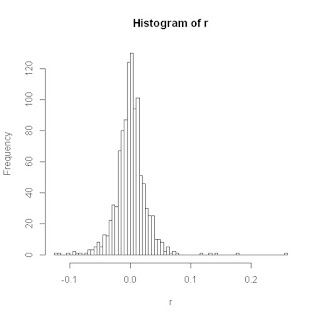
Para obtener una mejor compresión sobre la frecuencia relativa de los retornos diarios, vamos a trazar el histograma con el comando hist(). Podemos ajustar el número de células para agrupar datos mediante el argumento breaks

hist(r, breaks=100)

Los cuantiles de la distribución de retorno son interesantes desde la perspectiva de la gestión de riesgo. Podemos por ejemplo, determinar con un nivel de confianza del 99%, el valor en riesgo (VaR)  a un día desde un enfoque histórico.

quantile(r, probs = 0.01, na.rm = TRUE)

         1% 
-0.06524668 

Por lo tanto, la probabilidad de que el retorno sea inferior al -6.524868% en un día determinado es tan sólo el 1%. Pero si se produce ese día (y ésto ocurre 11 veces en los 1047 datos analizados) entonces 6.5% es la cantidad mínima que puede perder. Para ver los días que ésto ocurre hacemos:

r[r<=(-0.06524668)]
                  Delt.1.log
2012-05-21 -0.11637809
2012-05-22 -0.09325525
2012-05-29 -0.10115613
2012-06-01 -0.06562022
2012-07-16 -0.08382042
2012-07-26 -0.08868595
2012-07-27 -0.12436896
2012-09-24 -0.09491655
2013-10-08 -0.06924742
2013-11-18 -0.06708538
2014-03-26 -0.07187000

Si observamos en las noticias encontramos lo siguiente:

• 2012-05-21 es la primera semana se Facebook y no llena las expectativas de los inversionistas. 
• 2012-05-22 la empresa no ofrecerá certificados de papel de las acciones.
• 2012-05-29 problemas con la compra de Opera, una compañía de navegación móvil.
• 2012-06-01 Facebook sufrió cortes esporádicos durante unas tres horas.
• 2012-07-16 Facebook adquiere Spool Team para móviles. Tiene problemas con iOS y Android.
• 2012-07-26 y 27 Informes financieros no son tan buenos.
• 2012-09-24 Facebook publica por error mensajes privados de sus usuarios.
• 2014-03-26 Facebook y Google están gastando como locos en las tecnologías emergentes.

Hasta aquí el procesamiento de información en R con series temporales. Espero sea de utilidad. Cualquier comentario, pregunta, sugerencia es bienvenida. Hasta la próxima.